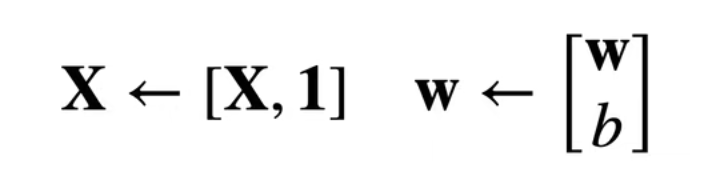线性神经网络----线性回归

线性回归

一、线性模型

线性假设

目标（房屋价格）可以表示为特征（面积和房龄）的加权和： $price=\omega_{area}\bullet area+\omega_{age}\bullet age+b$

$\omega_{area}$和$\omega_{age}$称为权重，$b$称为偏置项

偏置项的存在意义：使模型更灵活的拟合数据，具体而言就是偏置项的存在可以使模型能够适应数据的平移，即使自变量取零时，因变量也不一定为零，如果没有偏置项，模型只能通过原点拟合，模型的表达能力将会受到限制

数学表示

$\hat{y}=\omega_1x_1+...\omega_dx_d+b$ $\hat{y}$表示$y$的估计值，即预测结果

向量-向量形式：

$\hat{y}=\omega^Tx+b$

矩阵-向量形式：

$\hat{\mathbf{y}}=X\mathbf{w}+b$

其中$X^{n\times d}$表示特征集合，即样本矩阵，每一行是一个样本，有n个样本，$\omega^{d\times 1}$表示权重向量，可理解为每个特征的权重

所做工作

给定一个训练集，包括房屋的面积、房龄、房屋价格，寻找模型的权重$\omega$和偏置$b$， 然后作用在测试集上，使得根据模型做出的预测大体符合数据里的真实价格（损失函数最小）

有了目标（寻找模型参数$\mathbf{w}$和$b$）之后，我们还需要思考两件事情：

• 怎么去度量这个模型好坏或者说找到一种度量方式 A：损失函数
• 找到一种方法去提高模型的预测能力 A：梯度下降

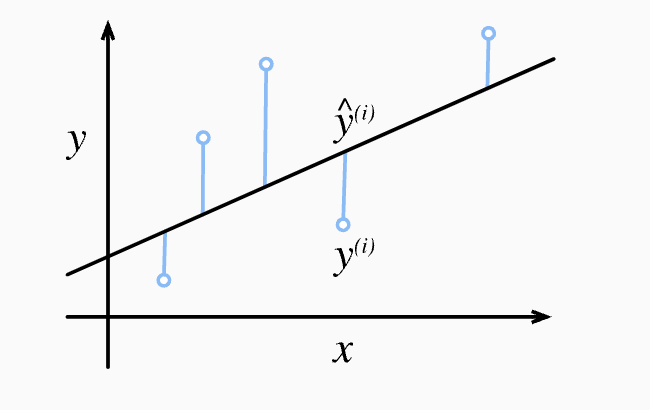
损失函数

损失函数，顾名思义，就是刻画真实值和预测值之间损失（差距）的函数，如果能找到其最小值，即说明我们的模型拟合程度好，通常来说损失函数选取非负数（很好理解，当损失为零0，完美拟合）。在回归问题中，我们选择均方误差损失函数：

$l^{(i)}(\mathbf{w},b)=\frac{1}{2} (\hat{y}^{(i)}-y^{(i)})^2$ 其中当第$i$个样本的预测值为$\hat{y}^{(i)}$，其相应的真实标签为$y^{(i)}$

如下图： 用线性模型拟合数据

但是前面我们说了既然是均方损失，为什么要均方呢？那均方体现在哪呢？

A1：我们要有大局观，着眼整个数据集，于是选择平均一下，况且，二次项看起来会使得损失函数很大

A2: $L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2=\frac{1}{2n}\|\mathbf{y}-X\mathbf{w}-b\|_2$

有了目标函数，我们的目标就可以抽象成： $\mathbf{w}^*, b^* = \operatorname*{argmin}_{\mathbf{w}, b}\ L(\mathbf{w}, b).$

解析解 （小插曲）

什么是解析解？🤓通过代数运算、推理和数学技巧，直接找到方程的解😋通常涉及到使用已知的数学公式、定理和规则来导出一个明确的表达式，该表达式表示方程的解。举个栗子，对于一元二次方程$ax^2 + bx + c = 0$的解，求根公式（懒得敲了）就是它的解析解，即不是近似的，是精确滴！

回到正题之前，我们先做一个事情，在矩阵-向量形式：$\hat{\mathbf{y}}=X\mathbf{w}+b$，这个形式看起来不太好算，我们化繁为简，将偏差加入权重：

则损失函数中的变为$\mathbf{y}-X\mathbf{w}-b$变为$\mathbf{y}-X\mathbf{w}$，损失函数变为$L(\mathbf{X},\mathbf{y},\mathbf{w})=\frac{1}{2n}\|\mathbf{y}-X\mathbf{w}\|_2$ 那么我们要做的事情就简化了， 现在我们只需要将$L$对$\mathbf{w}$求导，令其导函数为零，找到零点$\mathbf{w}_0$即可，以下是推导解析解的过程，涉及到向量对向量求导知识：

$\frac{1}{2n}\frac{\partial\|\mathbf{y}-X\mathbf{w}\|^2}{\partial\mathbf{w}}$

令$Z=\mathbf{y}-X\mathbf{w}$

$=\frac{1}{2n}\frac{\partial\|Z\|^2}{\partial{Z}}\frac{\partial{Z}}{\partial\mathbf{w}}$

$=\frac{1}{n}Z^\top(-X)$

$=\frac{1}{n}{(\mathbf{y}-X\mathbf{w})}^\top(-X)$

$=\frac{1}{n}{(X\mathbf{w}-\mathbf{y})}^\top{X}$

$=\frac{1}{n}{(\mathbf{w}^\top X^\top -\mathbf{y}^\top)} X$

$=\frac{1}{n}{(\mathbf{w}^\top X^\top X-\mathbf{y}^\top X)}$

损失是凸函数，令上式为零，即可得到最优解

$\mathbf{w}^* = (\mathbf X^\top \mathbf X)^{-1}\mathbf X^\top \mathbf{y}.$

值得一提的是，虽然这一结论我们用不到（显然我们有更先进的方法），但是还是很有必要学会基本推导滴（这也是一种乐趣不是嘛^ _ ^）

优化算法 随机梯度下降

基础不牢，地动山摇

建议先阅读 梯度下降 和 小批量随机梯度下降

我们这里采用小批量随机梯度下降：

$\mathbf{w} \leftarrow \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{\mathbf{w}} L^{(i)}(\mathbf{w})$

算法步骤如下：

• 初始化模型参数的值
• 从数据集中随机抽取小批量样本且在负梯度的方向上更新参数，并不断迭代这一步骤

从线性回归到神经网络

明明标题是中含有神经网络，但是却一直在说线性回归，那有什么关系呢？

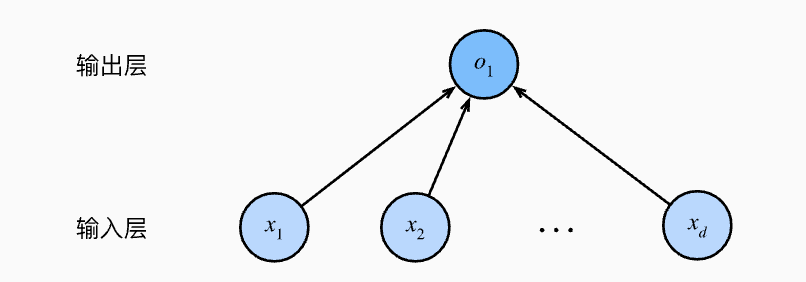
上图是线性规划的神经网络图，这个看着挺清楚地，有几个概念需要说明一下：

• 这个神经网络的层数为1（不考虑输出层），即是单层的
• 这是一个全连接层，即每个输入都与每个输出相连

---

二、手撕线性规划

直接调包就可以，为什么要学呢？

• 感受一遍整个实现过程，学习细粒度，认识更深刻
• 一定程度上锻炼coding和logic能力

-----------------------------正题开始--------------------------

1 生成数据集

def synthetic_data(w, b, num_examples):  #@save

    X = torch.normal(0, 1, (num_examples, len(w)))  # 每行是一个样本，每列是一个特征
    y = torch.matmul(X, w) + b    # y = Xw + b
    y += torch.normal(0, 0.01, y.shape)   # 加入具有正态分布的噪声
    return X, y

# 设置w,b的真实值，用来生成标签
true_w = torch.tensor([2, -3.4])
true_b = 4.2

# 得到特征和标签
features, labels  = synthetic_data(true_w, true_b, 1000)

这里说一下加入的噪声：$\mathbf{y}= \mathbf{X} \mathbf{w} + b + \mathbf\epsilon$

两个问题：

1）为什么要加入噪声？

为了考虑模型的不确定性和现实中的随机性。线性规划通常用于描述和优化具有确定性参数的问题，但在实际应用中，很多因素都是不确定的，可能受到各种随机影响。通过引入噪声，可以更好地模拟这种不确定性和随机性。

2）为什么噪声是服从正态分布的？

正态分布是一种常用的分布，因为根据中心极限定理，许多独立、相同分布的随机变量的和在样本容量足够大时会趋向于正态分布。这使得正态分布在模拟许多现实世界现象时非常有用。

顺便说一下，在高斯噪声的假设下，最小化均方误差等价于对线性模型的极大似然估计（有比较严格的数学证明，可以参考沐神的讲义），这也解释了损失函数为什么选择均方函数的原因

2 读取数据集

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))    # 0, 1, 2, ..., num_examples-1
    random.shuffle(indices)                # 样本的读取顺序是随机的

    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])  # 最后一次可能不足一个batch
        yield features[batch_indices], labels[batch_indices]    # 根据索引返回对应元素

这里不理解yield的可以参考下面的e.g.

# 对yield的理解
def my_generator():
    print("Generator is starting.")
    yield 1
    print("Generator is continuing.")
    yield 2
    print("Generator is finishing.")

# 创建生成器对象
gen = my_generator()

# 调用生成器的 next() 方法
value1 = next(gen)
print(f"Received value from generator: {value1}")

# 调用生成器的 next() 方法
value2 = next(gen)
print(f"Received value from generator: {value2}")

# 调用生成器的 next() 方法
# 由于生成器已经结束，再次调用将引发 StopIteration 异常
value3 = next(gen, None)
print(f"Received value from generator: {value3}")

3 初始化模型参数

batch_size = 10    # 定义批量大小，这里为了方便，就设置成了总样本数的因数
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True) # requires_grad=True表明需要求梯度
b = torch.zeros(1, requires_grad=True)

这里涉及到pytorch的自动微分知识，需要提前了解

4 定义模型

def linreg(X, w, b):
    return torch.matmul(X, w) + b

5 定义损失函数

def squared_loss(y_hat, y):             # 采用均方损失函数
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2   # 注意这里要将y变形成y_hat的形状

6 定义优化算法（小批量梯度下降）

def sgd(params, lr, batch_size):
    with torch.no_grad():     # 由于下面的loss.backward()函数会自动计算梯度，因此这里先将梯度清零
        for param in params:  # param是一个tensor
            param -= lr * param.grad / batch_size  # 注意这里更改param时用的param本身，而不是param.data
            param.grad.zero_()     # 梯度清零,否则会累加

7 模型训练

lr = 0.03
net = linreg
loss = squared_loss
num_epochs = 3

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # l是有关小批量X和y的损失
        l.sum().backward()        # 小批量的损失对模型参数求梯度
        sgd([w, b], lr, batch_size)  # 使用小批量随机梯度下降迭代模型参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')  # 记得要mean一下

结果：

epoch 1, loss 0.034300

epoch 2, loss 0.000119

epoch 3, loss 0.000050

8 估计误差

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

结果：

w的估计误差: tensor([ 0.0004, -0.0005], grad_fn=)

b的估计误差: tensor([0.0001], grad_fn=)

完整代码

%matplotlib inline
import random
import torch
from d2l import torch as d2l

# 生成数据集
def synthetic_data(w, b, num_examples): #@save
    '''生成 y = Xw + b + 噪声'''
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape(-1, 1)

true_w = torch.tensor([2.0, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

def data_iter(batch_size, features, labels): 
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]

batch_size = 10  

w = torch.normal(0, 0.01, size = (2, 1), requires_grad = True)
b = torch.zeros(1, requires_grad=True)

def linreg(X, w, b): #@save
    '''线性回归模型'''
    return torch.matmul(X, w) + b

def squared_loss(y_hat, y): #@save
    '''均方损失函数'''
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

def sgd(params, lr, batch_size): #@save
    '''小批量随机梯度下降'''
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  
        l.sum().backward()
        sgd([w, b], lr, batch_size)
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
        
print(f'w的估计误差{true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差{true_b - b}')

---

三、API实现

有了手动实现，简洁实现调用相关的包就可以了，各个步骤相较于之前简明很多，个人觉得也不用特别去记住这些包名，现查现用就可以了

import numpy as np
import torch
from torch.utils import data  
from d2l import torch as d2l
# 生成数据集
def synthetic_data(w, b, num_examples): #@save
    '''生成 y = Xw + b + 噪声'''
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape(-1, 1)

# 初始化参数并生成数据集
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

# 读取数据集
def load_array(data_arrays, batch_size, is_train=True):  #@save   is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据。
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)   # *表示可变参数
    return data.DataLoader(dataset, batch_size, shuffle=is_train)   # DataLoader是一个迭代器

# 设置批量的规模
batch_size = 10
data_iter = load_array((features, labels), batch_size)

# next(iter(data_iter))  验证数据集分批是否正确

# 定义模型
from torch import nn    # nn是神经网络的缩写
net = nn.Sequential(nn.Linear(2, 1))  # Sequential实例可以看作是一个串联各个层的容器,(2,1)表示输入特征数和输出特征数,Liner是Squential的一个模块

# 初始化模型参数
net[0].weight.data.normal_(0, 0.01)   # net[0]表示获取net中的第一个模块，即Linear模块，weight表示获取权重参数，data表示获取权重参数的值，normal_表示用正态分布的随机数填充权重参数的值
net[0].bias.data.fill_(0)   # bias表示获取偏差参数，fill_表示用0填充偏差参数的值

# 定义损失函数
loss = nn.MSELoss(reduction='mean')   # MSELoss表示均方损失函数，reduction表示损失函数的计算方式，mean表示求均值

# 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03)   # SGD表示小批量随机梯度下降，net.parameters()表示获取网络的所有参数，lr表示学习率
            
# 训练
num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')
        
# 得到误差
w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

结果：

epoch 1, loss 0.000251

epoch 2, loss 0.000101

epoch 3, loss 0.000101

w的估计误差： tensor([-0.0008, -0.0002])

b的估计误差： tensor([0.0006])

---

四、写在后面

到这里，本篇博客就结束啦！线性回归是基础，同样是我们打开深度学习大门（套路）的钥匙，掌握了这样的一套流程，后面的都是相应的扩展

另外，希望自己能将这个系列的博客一直更新（转载）下去，当然还是有自己的理解滴~

引用站外地址

内容参考自动手学深度学习

来自沐神 希望能有更多的自己的理解呀~